ANIMA Forbína

Byla nebyla jedna poptávková křivka …

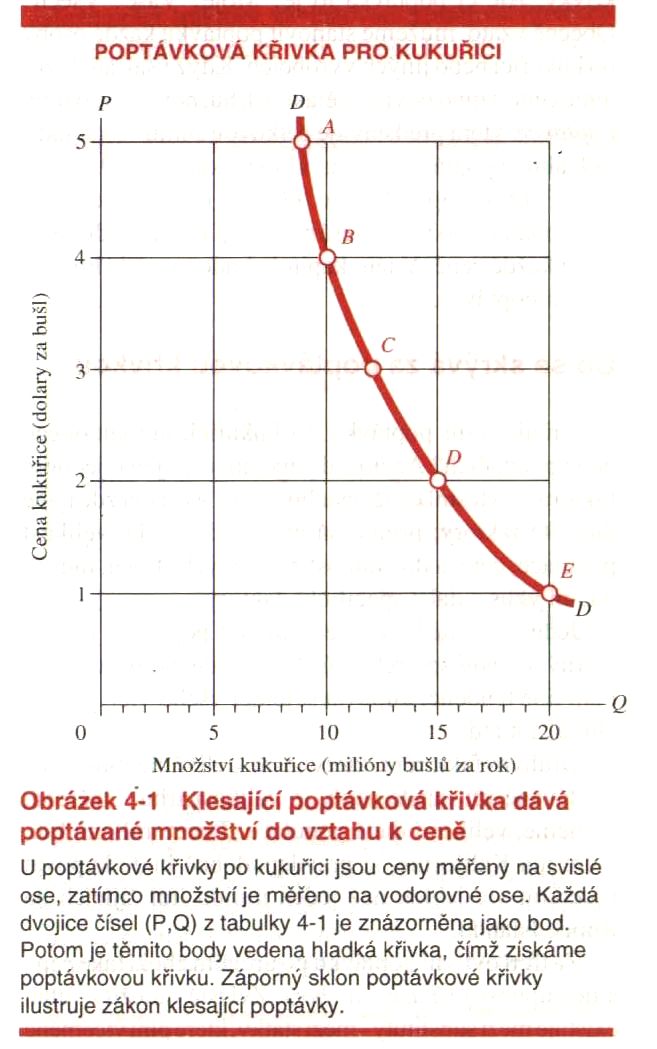
Vypadala jako ta, kterou jsem pro Vás naskenoval z často používané učebnice “Ekonomie” od Paula A. Samuelsona a Williama D. Nordhause.

Milé děti, stojíte-li u počítače, tak se pohodlně usaďte, protože v tomto a následujícím článku se dozvíte, jak to bylo dál. Dozvíte se podivuhodnou historii jednoho velkého nedorozumění. Možná si nakonec položíte otázku, jestli se skutečně jedná jen o nedorozumění, nebo jestli to náhodou nezakladá skutkovou podstatu něčeho vážnějšího.

Každý si mohl všimnout, vy také?

Obrázek, který jste viděl(a) na začátku, je v uvedené učebnici v místě, kde se čtenáři poprvé seznamují s poptávkovou křivkou. Přečtěme si, co se tam o ní píše.

“Každý si mohl všimnout, že množství určitého statku, které si lidé v daném čase kupují, závisí na jeho ceně. Čím vyšší je cena požadovaná za určité zboží, tím menší bude množství, které si lidé budou ochotni koupit. A naopak, za jinak stejných podmínek, čím nižší bude tržní cena daného zboží, tím více jednotek budou lidé chtít koupit.

V každém okamžiku tedy existuje zcela určitý vztah mezi tržní cenou zboží a množstvím, které jsou kupující ochotni si koupit. Tento vztah mezi cenou a nakupovaným (poptávaným) množstvím se nazývá poptávková funkce nebo poptávková křivka.”

Potom hned následuje tabulka 4-1, která je překreslena na obrázek 4-1 uvedený nahoře. O tabulce se v textu říká: “Tabulka 4-1 ukazuje hypotetickou poptávkovou funkci.” Pozor, nikoli skutečná data, ale něco, co si autoři vymysleli.

Nic víc se tam nedozvíte. Od tohoto okamžiku se předpokládá, že studenti budou o reálné existenci poptávkové funkce přesvědčeni, a co víc, budou přesvědčeni, že poptávková křivka je taková pěkná, klesající křivka, jako jsme viděli na úvodním obrázku. Podívejte se ještě jednou na citovaný text. Připadá Vám přesvědčivý? V čem je přesvědčivější než text následující?

“Každý si mohl všimnout, že každý den ráno slunce vychází na východě, až do poledne stoupá po obloze, pak klesá, až večer zase zapadne. Z toho je vidět, že Slunce obíhá po dráze kolem Země a doba oběhu je jeden den.”

Argumentace je velmi podobná - nejprve se říká, že každý si mohl čehosi všimnout a pak se jako houska na krámě nabízí něco, o čem se tvrdí, že se tím to pozorování vysvětluje. Studenti kurzů ekonomie si obvykle tuhle housku koupí a pak se to s nimi většinou táhne celý život. Jak by také ne, když velká část toho, co později v kurzu probírají, “zákon klesající poptávky” předpokládá.

Začít se pozorněji dívat a myslet

Podívejme se nejprve na druhý argument, o němž víme, že je špatně - argument o “zákonu jednodenního oběhu Slunce”. Jak se dostaneme ze zajetí sofistiky, na níž je založen? Tak, že se pozorněji podíváme, čeho že si to měl každý všimnout. Při pozorování východů slunce zjistíme, že slunce vychází každý den  trochu jinde. Tam, kde vyšlo dnes, vyjde znovu až za 365 dní. Taková pečlivá pozorování nakonec vyloučí primitivní představu o jednodenním oběhu Slunce kolem Země a po nějaké době zjistíme, že východy a západy slunce vůbec nesouvisí s obíháním Slunce kolem Země, ale s tím, že se Země otáčí. Nakonec třeba dojdeme i k tomu, že Země obíhá kolem Slunce.

Stejně pozorně začněme pracovat s prvním argumentem, který směřuje k “zákonu klesající poptávky”. Jak je to s pozorováním, že “Čím vyšší je cena požadovaná za určité zboží, tím menší bude množství, které si lidé budou ochotni koupit”? Podíváte-li se na různé typy zboží (určitě Vám to v poslední době neuniklo například ve zprávách o cenách zlata) a na údaje o tom, jaká je poptávka při určité ceně, zjistíte velké odchylky od “zákona poptávky” - například ceny dlouhodobě stoupaly a současně stoupala poptávka. Vypadá to, že poptávková křivka (pokud to vůbec bude křivka!!) nebude taková pěkná klesající křivka jako na úvodním obrázku, ale spíš něco takového:

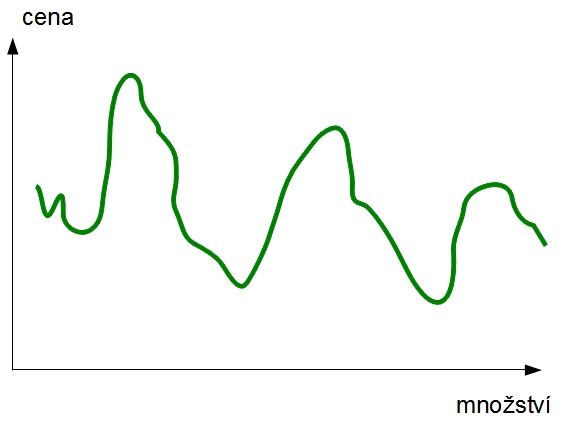
Tímto a následujícím článkem směřujeme k tomu, abychom připomněli, že už přes půlstoletí je známo, že takové “poptávkové křivky”, jako vidíme na tomto obrázku, jsou spíš pravidlem. Takové, jako ukazoval úvodní obrázek, se možná hojně vyskytují někde za “devatero horami a devatero řekami”, v našem světě jsou čímsi poměrně nevídaným.

Možná jste si hned uvědomil(a), že takováto “reálná” poptávková křivka neudává funkci ceny - za stejnou cenu jsou lidé ochotni si koupit (v různých okamžicích) různá množství zboží. Co je horší, takováto křivka nám pokazí mýtický obrázek “zákona nabídky a poptávky”, o němž jsme psali v minulém článku:

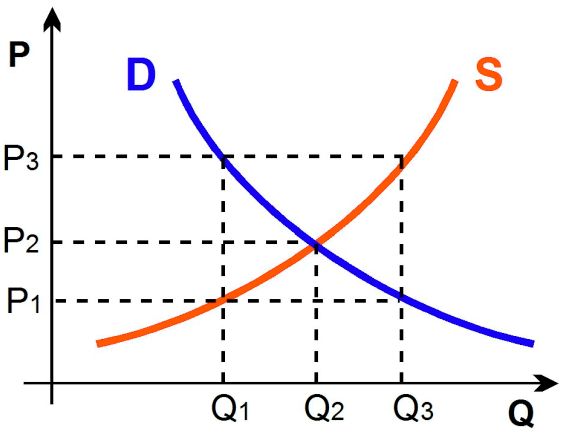
Představte si, že v něm nahradíte “ukázněnou” (modrou) klesající poptávkovou křivku tou naší “reálnou” (zelenou) z předchozího obrázku. Ta se nám může s (červenou) nabídkovou křivkou protnout hned v několika různých bodech a kde bude ona jednoznačně určená cena a množství, kterou určí “zákon nabídky a poptávky”?

Uvážíme-li, co všechno i v úvodní učebnici ekonomie závisí na “zákonu klesající poptávky”, nechce se věřit, že by byl založen jen na takovém logickém skoku, jaký jsme si mohli přečíst, zvláště když mu empirická zjištění zrovna nenahrávají. Možná se vysokoškolským studentům v úvodním kurzu předkládá jako článek víry, jak jsme to viděli, ale někde za scénou si to odborníci odpracovali a platnost “zákona poptávky” pořádně vědecky odvodili.

Na to se teď podíváme.

Krok za krokem, nebo kotrmelec za kotrmelcem?

Popíšu Vám teď nejpodrobnější cestu vedoucí k poptávkové křivce, jakou se mi podařilo najít, a u každého důležitého kroku se na chvilku zastavíme. Znáte-li nějakou jinou cestu, stejně podrobnou, budu Vám vděčný za upozornění.

Začneme od něčeho nezpochybnitelného - od pozorování, že člověk stále volí mezi různými možnostmi. Jak volí? To je někdy těžké říci. Dnes se rozhodne, že se nebude dívat v televizi na film, ale raději se půjde projít. Možná by se zítra rozhodl obráceně, i kdyby volil mezi stejným filmem a stejnou procházkou a může být téměř nemožné vystopovat, proč se rozhodl jinak.

Poměrně velký logický skok uděláme, když přijmeme tezi, že člověk volí vždy tu možnost, která přináší větší užitek. Tuto představu rozpracoval Jeremy Bentham, o němž jsem se zmiňoval minule.  Domníval se, že užitek, který jednotlivé možnosti přinášejí, je možné změřit. Zhruba řečeno takto: jestliže se rozhoduji, zda jít do práce, poměřuji bolest, kterou mi to způsobí (pracovat - jaká hrůza!) s potěšením, které mi to přinese - dostanu peníze, za něž si mohu pořídit, co se mi líbí. Potěšení i bolest změřím, obě čísla od sebe odečtu a výsledek je užitek, který mi den v práci přinese.

V knížkách často najdete nějaký takovýto obrázek:

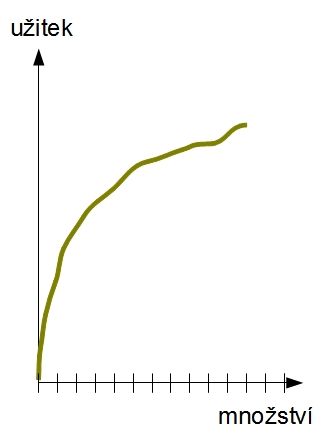
Ve tvaru křivky je zakódován důležitý postulát Benthamovy morální filozofie: lidé jednají podle zásady “více je vždy lépe”. I když se tím trochu vracíme k tématu předchozích článků, je důležité si uvědomit, jak je to vzdáleno každodenní zkušenosti. V jistém okamžiku si normální člověk řekne “a dost” a příslušné zboží začne odmítat. Je pravda, že se zde uplatňuje substituční efekt: jestliže cena šampaňského klesne pod cenu vody, jeho poptávka stoupne, protože se v něm lidé začnou koupat - šampaňské začíná substituovat vodu.

V komentáři pod článkem “Zveme Vás na žně” napsal Tomáš na toto téma krásnou parodii - co všechno mohou substituovat párky. Můžete je používat jako těžítko, zkoušet z nich vyrobit přímotop, a podobně. V reálném životě byste i v případě substituce na uvedené křivce nejpíš zaznamenali zhoupnutí - u určitého množství Vám to zboží začne překážet, až od jistého vyššího množství dává substituce smysl. Navíc i  substituce má své meze. Představte si, že se deset párků prodává za korunu. Všude se válejí zelené, plesnivé, páchnoucí párky a přesto se všichni lidé stále obracejí na uzenáře s návrhy: “Udělejte mi cenu, dejte mi 50 párků za korunu a já od vás vezmu dalších tisíc párků”. Není to fikce?

Teď se na ten obrázek ještě jednou podívejme a ověřme, že mu správně rozumíme. Když už jsme se dostali k párkům, tak se jich ještě chvíli držme - na vodorovné ose vynáším počet párků, na svislé ose je znázorněno, jaký užitek pro mne má příslušné množství párků.

První párek pro mne má určitý užitek, druhý k němu přidá užitek o něco menší a tak dále. Až takový graf někde uvidíte, všimněte si, že na svislé ose nebývají znázorněné žádné jednotky. To vyjadřuje jakousi ostýchavou distanci od Benthamových představ. Bentham očekával, že užitek bude možné měřit a vyjadřovat v určitých jednotkách, jako se měří fyzikální veličiny. Stanoví se jednotka, dejme tomu 1 juž (jednotka užitku) a užitek věcí se bude vyjadřoval v južích. Už zmíněný párek má pro mne užitek 2,8 juž, pozorování východu slunce 1,3 juž, sledování schůze parlamentu -17,4 juž, atd.

Je těžké tuto představu delší dobu rozvíjet a nezačít se smát. Proto bývá na té kolmé ose napsáno jen “užitek” a o hodnotách se nemluví - většinou se explicitně říká, že číselné hodnoty nejsou důležité, důležité je jen srovnání - co má větší a co menší užitek. Za moment uvidíme, jak se južů elegantně zbavit.

Před chvílí jsem napsal, že uděláme velký logický skok, ale možná je to pořádný kotrmelec, nejen skok.  Proč? Jestliže totiž od faktu, že se člověk rozhoduje, přejdeme k představě, že se rozhoduje podle užitku, který je možné vynést na číselnou osu, potom tím mlčky nabalujeme další předpoklady, například předpoklad tranzitivity rozhodování, o níž jsem psal v minulém článku: jestliže A v mých očích vítězí nad B (má větší užitek) a B vítězí nad C, potom A vítězí nad C. V minulém článku jste si mohli přečíst, jak na ten předpoklad doplatil Bart Simpson. Tím předpokladem zakazujeme věci, které v reálném světě existují - nebo chcete-li, začínáme se stěhovat z reálného světa někam jinam. Můžete se sami zamyslet nad tím, co dalšího, krom předpokladu tranzitivity jsme v tomto kroku nabalili.

Teď to začne být zajímavé - od jednoho druhu zboží přejdeme ke kombinaci několika druhů zboží. Kolik južů vám přináší sledování západu slunce kombinované s popíjením půllitru piva a poslechem písně “Holky z naší školky”?

Už nás také čeká jen jeden obrázek. Jestli se vám při pohledu na něj udělá špatně, nedívejte se na něj a zkuste vystačit s textem, který je pod ním. (Pak se k obrázku možná rád(a) vrátíte.)

Zákon poptávky po rohlících

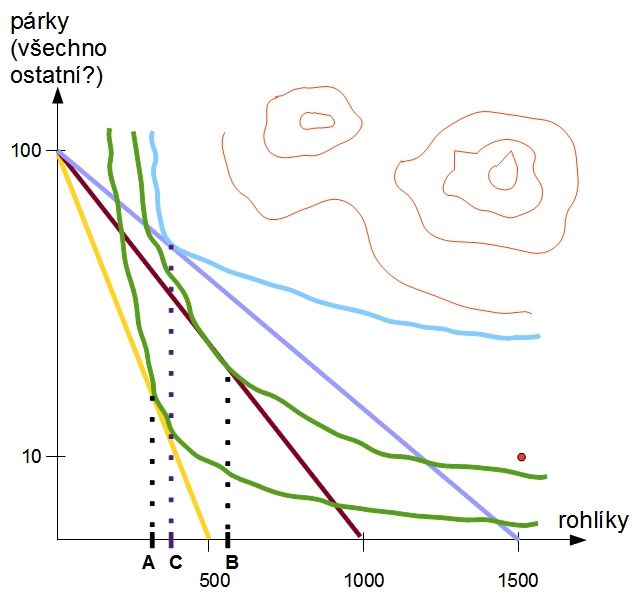
Budeme teď přemýšlet současně o dvou druzích zboží - párcích a rohlících. Kdybyste sledovali podrobné odvozování zákona klesající poptávky pro rohlíky, setkali byste se s podobným obrázkem - jenom na svislou osu bychom vynášeli místo párků agregaci všeho ostatního, co kromě rohlíků svět přináší. Jenomže v jakých jednotkách “všechno ostatní” na svislou osu vynášet? Nebudeme se tím tady zdržovat, pár stránek by to zabralo, ale možná na to na konci přijdete sami. Zůstaneme pro jednoduchost u párků.

Každý bod v kvadrantu znázorňuje určitou kombinaci rohlíků a párků. Například červený bod vpravo dole symbolizuje kombinaci 10 párků a 1500 rohlíků. Spolu s Benthamem si teď představte, že pro každý bod kvadrantu je určen užitek, který Vám (konstruujeme poptávkovou křivku jednoho konkrétního člověka) přináší příslušná kombinace párků a rohlíků.

Dejme tomu, že kombinace 1500 rohlíků a 10 párků Vám přináší užitek 2875,53 južů. V tom případě by kolmo nad červeným bodem ležel ve výšce 2875,53 příslušný užitkový bod. Dohromady mohou všechny užitkové body vytvořit jakousi plochu, která se vznáší nad příslušným kvadrantem. Tvar té plochy můžete znázornit pomocí vrstevnic, jak to vidíte na obrázku. (Kromě červených vrstevnic tam vidíte ještě jednu modrou a dvě zelené vrstevnice.) Co charakterizuje body ležící na jedné vrstevnici? Všem odpovídá stejný užitek. Z hlediska užitku je Vám tedy jedno (jste v této otázce indiferentní), jestli zvolíte jednu nebo druhou kombinaci ležící na stejné vrstevnici. Proto se takovýmto vrstevnicím v ekonomii říká indiferenční křivky.

Scéna je připravena, začneme odvozovat zákon klesající poptávky.

Samuelsonův bagr

Nejprve vám musím s politováním oznámit, že červené vrstevnice musí z našeho obrázku zmizet. Proč? Zakazují je čtyři Samuelsonovy axiomy racionálního chování spotřebitele, o nichž jsem se zmínil v minulém článku. (Chudák Bart Simpson doplatil na to, že respektoval jeden z nich, pamatujete?) Podle oněch axiomů se vám nesmí stát to, co by se stalo v krajině na našem obrázku: vyrazili byste z levého dolního rohu, směřovali byste po přímce přibližně na SV a cestou byste vystoupali na jeden z kopečků, které na mapě vidíte, pak byste z něho sestoupili a pokračovali dál. To se nesmí stát - podle zmíněných axiomů platí zásada “více je vždy lépe”, takže musíte pořád stoupat, žádný ani malý sestup nepřichází v úvahu. Krajina vybagrovaná Samuelsonovými axiomy je jeden nekonečný táhlý svah a na její mapě se objevují jen vrstevnice, které vypadají jako ta modrá a dvě zelené na našem obrázku.

Přijetím axiomu tranzitivity a tří dalších axiomů zakážeme spoustu věcí, které v našem světě existují. Ptáte se, proč to děláme? Protože chceme vytvořit svět, kde platí zákon klesající poptávky, hrome! Jestli mě nepřestanete rušit, tak Vám to nedovyprávím. A už jsme u toho nejhezčího!

Kolik máte peněz a jaké jsou ceny?

Chceme-li teď začít malovat Vaši poptávkovou křivku pro rohlíky, potřebujeme vědět, kolik můžete utratit peněz a jaká je cena rohlíků a párků. Aby se to lépe počítalo, předpokládejme, že máte 1000 Kč, rohlík stojí 2 Kč a párek 10 Kč. Tomu odpovídá oranžová úsečka na obrázku. Její krajní body odpovídají kombinacím (100 párků, 0 rohlíků) a (0 párků, 500 rohlíků). Body úsečky jsou tvořeny právě všemi kombinacemi počtu párků a rohlíků, které můžete při daných cenách koupit za 1000 Kč. Jestliže jste měl(a) na základní škole dobrou učitelku nebo učitele matematiky, vidíte to hned (a věnujte paní učitelce nebo panu učiteli vděčnou vzpomínku). Jestliže to hned nevidíte, můžete vzít tužku a papír, chvilku si s tím pohrát a přesvědčit se, že to tak opravdu je.

Kterou kombinaci zvolíte? Tu která Vám přinese největší užitek. Která to je? No přece ta, která se dotkne nejvýše položené vrstevnice mezi těmi, na něž úsečka “dosáhne”! V našem případě je to ta níže položená zelená vrstevnice. Přečtete si, kolik rohlíků odpovídá kombinaci v bodu dotyku - v našem případě je to A rohlíků.

Můžeme si tedy někde vedle na papír začít vykreslovat poptávkovou křivku. Při ceně 2 Kč za rohlík budete poptávat A rohlíků. Jestliže nyní rohlíky zlevníme na polovinu, zatímco nezměněna zůstane cena párků i množství peněz, které máte k dispozici, bude této situaci odpovídat hnědá usečka. Ceně 1 Kč za rohlík tak bude odpovídat poptávka po B rohlících. Cena klesla, poptávka se zvýšila, jak to u “správné” poptávkové křivky má být. (Jestliže dokážete vyřešit, jak na svislou osu vynášet “všechno ostatní”, máte už v ruce nástroj jak konstruovat poptávkovou křivku - fixujete cenu “všeho ostatního”, pohybujete cenou rohlíků a hledáte body dotyku příslušných indiferenčních křivek.)

Začíná se Vám to líbit? Možná Vás hned na začátku při pohledu na systém vrstevnic zarazilo, že nejsou popsány “nadmořskou výškou”, jak to u map bývá. Teď je vidět, že je to zbytečné. Úplně stačí soustava indiferenčních křivek - k tomu, abychom určili vrstevnici, která se dotýká příslušné úsečky, nepotřebujeme znát číselnou hodnotu užitku, která vrstevnici odpovídá. Zbavili jsme se tedy noční můry zvané juž.

Také je vidět, proč nemohly na mapě zůstat červené vrstevnice. Podívejte se třeba na tu, která je na našem obrázku nejníže položená. Vidíte, že jistá úsečka by se jí dotkla ve dvou bodech - popsaný mechanismus vytváření poptávkové křivky by pak selhal. V řádně vybagrované krajině se to nestane.

Sice jsme se omezujícími předpoklady pořádně vzdálili od reálného světa, ale vytvořili jsme svět, kde se dá poptávková křivka konstruovat a zdá se, že je klesající, jak jsme si přáli.

Opravdu? Bohužel na našem obrázku vidíme, že další zlevnění rohlíků nás probudí z krásného sna. Zlevníme dále rohlíky, takže jich za 1000 Kč koupíme 1500 a situaci znázorňuje fialová úsečka. Jenomže teď se snížení ceny projevilo snížením poptávky (C je menší než B).

Zjišťujeme, že i v řádně vybagrované krajině můžeme popsanou metodou dostat poptávkovou křivku, která bude chvíli klesat, chvíli stoupat. Na jakou zradu jsme tu narazili?

Vliv příjmu

Na stopu toho, co tu nastalo, Vás může přivést podrobnější zkoumání indiferenčních křivek, které jsou zde ve hře - svah strměji stoupá směrem k vyššímu počtu rohlíků než směrem k většímu počtu párků. Je to něco, s čím se v nějaké podobě setkáváme často. Člověk potřebuje v první řadě zahnat hlad. Má-li málo peněz, docílí toho tak, že většinu peněz vydá za rohlíky. Jestliže dojde ke snížení cen rohlíků, má to podobný efekt, jako by se mu zvýšil příjem - může si dopřát více párků a díky tomu už nebude kupovat tolik rohlíků. Tomu se říká vliv nebo účinek příjmu, někdy také důchodový efekt.

V masivním měřítku něco takového prý bylo možné pozorovat například během velkého hladomoru v Irsku v polovině 19. století, během něhož zemřelo přes milión lidí. Ačkoli cena brambor rostla, poptávka po nich se neustále zvyšovala - lidé už si nekupovali nic jiného než brambory, jen aby zůstali naživu.

Existuje metoda, jak poptávku očistit od vlivu příjmu a získat takzvanou kompenzovanou poptávkovou křivku. Ta už snad konečně bude mít kýžený klesající tvar.

Dosáhli jsme svého. Ovšem za cenu velkých čistek. Můžete si je projít. Nejprve jim  za oběť padla schopnost říci dost a pak to šlo jedno za druhým až jsme nakonec svůj svět očistili od vlivu příjmu - něčeho s čím se miliardy lidí potýkají každý den.

Odfiltrovali jsme všechny ty nehezké poptávkové křivky, které chvíli klesají, chvíli stoupají a zůstaly jen ty, které se řídí “zákonem klesající poptávky”.

Dosud jsme se ovšem zabývali jen poptávkovými křivkami jednotlivců. Nadešel čas je agregovat. Na první pohled to může vypadat jako snadná záležitost - křivky jednotlivců se prostě posčítají. Tak si to zřejmě  představoval i Bentham. Jestliže Honza je při ceně párku 10 Kč ochoten koupit 5 párků a Božka je při stejné ceně ochotna koupit 3 párky, potom ti dva jsou při uvedené ceně dohromady ochotni koupit 8 párků.

Takže úvaha vypadá takto: vezmeme poptávkové křivky všech jednotlivců, sečteme je bod po bodu a výsledkem bude agregovaná poptávková křivka. Jestliže jsme (za cenu velkých obětí) dospěli k tomu, že křivky jednotlivců jsou klesající, bude i agregovaná křivka klesající.

Omyl. Tato úvaha není v pořádku.

To už si necháme na příště. Nejen ukážeme, v čem je ta úvaha špatně, ale podíváme-li se do historie, zjistíme, že nás to zavede až k VŠ (velkému švindlu).

Kdy to bude

Jsem rád, že se mi podařilo aspoň tuto první část zveřejnit ještě před ANIMA Instruktáží “Rozumět poptávce”, která bude příští týden, ve čtvrtek 20. října 2011.  Budu se snažit, aby druhá část následovala co nejdříve, ale nemohu zaručit, že to bude ještě před tou instruktáží. Účastníci instruktáže se to samozřejmě dozví všechno s plnou parádou - zde jsme se dotkli jen základů a i tak ten článek nepatří k nejkratším.

Internetové adresy pro přihlášky na ANIMA Instruktáže zůstávají v platnosti:

• klikněte zde a zobrazí se Vám leták sloužící zároveň jako faxová přihláška, kterou si můžete vytisknout,
• klikněte zde a můžete se přihlásit on-line.

Zpět na úvodní stránku

Tento článek byl zveřejněn 12/10/2011 v 10:36 am a je založen v kategorii Myšlení, Manažerské počty, Vzdělávání. Můžete sledovat odpovědi na tento článek prostřednictvím RSS 2.0 spojení. Můžete poslat odpověď, nebo sledovat ze svých vlastních stránek.