Zveme vás na žně
V první půli tohoto roku jsme se věnovali dvěma hlavním tématům:
- manažerským móresům,
- otázce, jak se zdokonalovat v umění myslet.
Teď přišla doba, abychom sklízeli plody obou témat, a to na poli, které je prakticky velmi důležité pro jednotlivce i pro firmy. Jak to bude vypadat, se dozvíte v tomto článku.
Už je to skoro tři roky, kdy jsme tady ve Forbíně zareagovali na finanční krizi článkem “Jak se připravíte na krizový let?“, který jsme zakončili výzvou k posvícení - na co by si firmy měly posvítit, chtějí-li obstát v krizovém období.
Od té doby jsme nezaháleli a s pomocí některých z vás jsme počáteční úvahy dále zpřesňovali. Nakonec jsme se poněkud překvapivě dostali ke dvěma tématům - výpravě do oblasti morální filozofie a k téměř zapomenuté metodě, jak se učit myslet - k takzvanému triviu. Pokud jste se toho účastnili, vzpomenete si, že jsme se při tom opakovaně setkávali se slovy “myslet naplno”.
Teď nás čeká sklizeň - vyzkoušet to, s čím jsme se seznámili, na něčem, co je dostatečně významné a co má nepochybnou praktickou důležitost. Skutečně nehodláme troškařit. Na co se chystáme, vám napoví následující citát z knihy australského ekonoma Steva Keena. Přečtěte si ho pozorně, máme v úmyslu se k němu ještě vrátit.
“Víra, že ekonomická teorie je zdravá, a že jen ona bere v potaz ‘velký obraz’, je hlavním důvodem, proč ekonomie získala takovou nadvládu nad veřejnou politikou. Říká se nám, že ekonomové vědí nejlépe, co je dobré pro společnost, protože ekonomická teorie ví, jak funguje tržní hospodářství, a jak je možné jeho fungování zlepšit k nejvyššímu prospěchu všech. … Když občas ekonomika neodpoví, jak ekonomická teorie předpověděla, je to proto, že příslušní zákonodárci aplikovali teorii chybně, nebo používali zastaralou ekonomii.
Kecy.”
(Steve Keen, Debunking Economics - The Naked Emperor of the Social Sciences)
Vidíte, že se opět dotýkáme i důležitého fenoménu keců, kterému jsme se už zde na Forbíně věnovali. Pro přesnost uvádím, že Keen v originále použil slova “bunkum”, nikoli “bullshit”. Význam je ovšem stejný.
Věříte na protínání křivek nabídky a poptávky?
Podzimní program nebude předpokládat, že účastníci absolvovali kurz ekonomie - vše potřebné vyložíme - v tuto chvíli však náš záměr lépe docení ti z vás, kterým už někde ve škole nebo na školení na nějakém takovémto obrázku
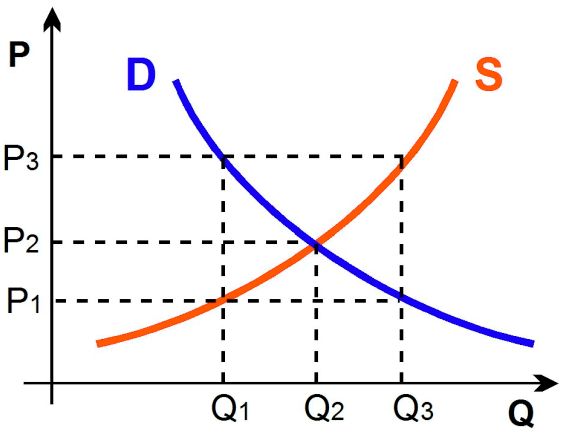vysvětlovali, jak cena a množství zboží na trhu směřuje k rovnovážnému stavu danému průsečíkem křivek nabídky a poptávky.
Věříte tomu? Proč? Zkuste si vzpomenout, jak vás o tom přesvědčili, nebo si zalistujte ve své oblíbené učebnici.
Proč by měla být křivka poptávky klesající? Co když není? Co když je tak podivně pokroucená, že křivku nabídky protne ve více bodech? Odpovídá křivka poptávky něčemu reálnému? Nebo je to jen hezký mentální model bez vztahu k realitě?
V jednom z následujících článků (ještě před zahájením podzimní série instruktáží) ukážeme, že ty otázky nejsou nesmyslné a odpověď na ně není vůbec snadná, budeme-li se snažit udržet na úrovni “myšlení naplno”, jak jsme o něm mluvili ve třech instruktážích věnovaných logice.
Ještě jeden příklad i pro ty z vás, kterým výše uvedený obrázek zatím nic neříká. Představte si dvě možné situace. První možnost: určitý produkt vyrábí monopol. Druhá možnost: stejný produkt vyrábí množství malých vzájemně spolu soutěžících firem. Která možnost je pro zákazníky lepší? Asi vás napadnou různé důvody, proč by měla být lepší druhá možnost. Je mezi nimi také důvod, že druhá možnost povede k tomu, že se produkt bude nabízet za menší cenu a ve větším množství? Proč si to myslíte? Máte dojem, že se to dá dokázat z ekonomické teorie? Odkud jste ten dojem získali?
Co když jsou to jen kecy, jak o nich píše Keen? Nebo máte dojem, že to prostě dá rozum? I rozum, který “myslí naplno” a logicky přesně? Schválně si to tedy zkuste zdůvodnit pomalu a bez logických skoků.
Snad už začíná být vidět, do čeho se hodláme pustit. Nechystáme se budovat alternativní ekonomickou teorii, ale pod palbou “disidentní ekonomické munice” budeme usilovat o to, abychom několika základním konceptům hlouběji porozuměli.
Jak to bude probíhat
Chystaná série instruktáží bude volně navazovat na obě předchozí série z 1. a 2. čtvrtletí tohoto roku. Slovo “volně” znamená, že instruktáže budou srozumitelné i těm, kdo se předchozích sérií neúčastnili. Nejspíš však neproniknou do takové hloubky, jako ti, kdo se jich účastnili - ti uvidí, jak velká návaznost tam je.
Těžiště celé série bude ve třech instruktážích, které budou věnovány právě vyjasňování několika základních konceptů panující ekonomické teorie. Charakter těchto instruktáží bude velmi interaktivní. Na začátku vyložím pojmy, o něž se bude jednat, a to způsobem srozumitelným i pro ty, kdo žádný kurz ekonomie neabsolvovali, i základní poučky uváděné zpravidla hned zkraje ekonomických kurzů. Pak už budu dělat jen ďáblova advokáta, kterému budete mít možnost dokazovat, že ony poučky nejsou jen kecy.
Co nám to přinese? Umožní nám to ve velkém stylu vyzkoušet, jak “myšlení naplno”, jímž jsme se opakovaně zabývali v předchozích dvou sériích, pomáhá hlouběji porozumět velmi důležitým pojmům. Co víc, některé argumenty občas používané na podporu výše zmíněných pouček se opírají o představu fungování firem, které je vyloženě škodlivé v dobách, kdy firma nemá dostatek zakázek. Předpokládám, že tyto představy během diskuse dostatečně provětráme.
Efekt zmíněných tří instruktáží zesílí dvě další instruktáže - jedna, která jim bude předcházet, a jedna, která celou sérii uzavře.
První instruktáž
První instruktáž bude mostem spojujícím tuto sérii se sérií předchozí. Zatímco v předchozí sérii jsme se hlavně zabývali tím, jak bychom měli myslet, teď to dáme do souvislosti s tím, jak obvykle myslíme. Budeme se například zabývat tím, proč v některých záležitostech je rozumné dát i na lidi, kteří logicky myslet zjevně neumějí, a jejichž názory v jiných oblastech je lépe nebrat vážně.
Budeme se také zabývat tím, čemu a jak věříme. To se nám hodí i v následujících instruktážích. Ani z citátu Steva Keena o kecech obsažených v panující ekonomické teorii totiž neplyne, že byste se měli dívat skrz prsty na ekonoma ve vaší firmě. Možná je to ten nejcennější člověk, kterého tam máte, a každé jeho slovo byste měli brát s plnou vážností. Věří váš ekonom na “protínání křivek nabídky a poptávky”? Jestliže ano, jak na ně věří?
Závěrečná instruktáž série
Poslední instruktáž celou sérii uzavírá a v jistém smyslu navazuje na sérii instruktáží o GTD (hospodaření s časem), které jsme se věnovali před několika lety. Od té doby jsme tuto metodu měli příležitost obohatit o několik praktických zkušeností, ale hlavně všechny tři série instruktáží z tohoto roku umožňují GTD dostat na vyšší úroveň. Úsilí o to, aby nám “věci odsýpaly” (GTD = Getting Things Done) povýšíme na úsilí o to, abychom měli důvody k radosti (GRJ = Getting Reasons for Joy). Tomu je vhodné se cíleně věnovat, protože
- v nejbližších letech dosavadních důvodů k radosti možná bude ubývat,
- GTD je zjevně jen speciálním případem GRJ a
- témata tří letošních sérií tvoří velmi dobrý základ pro GRJ.
Termíny, ceny
Program podzimní série instruktáží oznámíme začátkem září. Už teď jsou však pevně dané
- termíny instruktáží: 29. 9., 20. 10., 10. 11., 24. 11., 8. 12. 2011,
- ceny: zlatá permanentka stojí Kč 12 000 (+ DPH), cena jednotlivé instruktáže je Kč 3 000 (+ DPH).
16/08/2011 v 11:09 am
Zajímavé myšlenkové cvičení. Akorát se mi nelíbí, že se ty křivky nabídky a poptávky všichni kreslí odnikud nikam. Určitě budou mít v krajních oblastech zajímavější tvar a ten pak může i dát odpověd, jak to bude např. s tím monopolem.
16/08/2011 v 11:39 am
Petrovi:
Zjevně jste se vydal správným směrem. Chystám se v následujících článcích soustředit na jedno téma - poptávkovou křivku - které přijde na řadu v říjnu.
Můžeme ho tedy začít pomalu oťukávat už tady v komentářích.
Kreslení “odnikud nikam”, jak to nazýváte, může být příznakem jakýchsi rozpaků - navozuje to představu, že by se křivka mohla asymptoticky blížit k osám, ale naplno se to raději netvrdí.
Je to jako u křivky “mezního užitku”, která číhá v pozadí. Mám-li hlad, má pro mě párek v rohlíku velký užitek. Druhý párek už má menší užitek. Třetí párek má opět o něco menší (ale stále kladný) užitek.
A tady se řekne “a tak dále”, jinak by se musely začít “kecat hlouposti”.
16/08/2011 v 4:49 pm
Je to moc hezké myšlenkové cvičení. Zatím jsem si neudělal čas, abych si na to sednul s tužkou a papírem, ale jen to, co se mi honí hlavou, když jdu po chodníku, stojí za to (tedy alespoň pro mě). Uvědomil jsem si, kolik myšlenkových kroků je ve hře, kolik sylogismů bych potřeboval k tomu, abych došel k obvyklým závěrům.
Křivky se kreslí jako spojité, ale množství (vlastně i cena) je vždy v nějakých jednotkách - kvantované. Co když tu funguje něco podobného přechodu od newtonské fyziky ke kvantové a v okrajových případech (jednotky kusů) bude všechno jinak (Modrý Mauritius, Mona Lisa)? Co by se stalo, kdyby ze dne na den vymřeli všichni filatelisti?
Nakolik je ekonomie objektivní? Mohu se rozhodovat, jestli si koupím A nebo B nebo C nebo nic (to je subjektivní), ale na to, abych si koupil A, B i C prostě nemám dost zdrojů (to je objektivní).
Bylo by potřeba vyjasnit, co křivky vlastně znázorňují. Zejména u křivky nabídky nevím, zda se dá mluvit o křivce nabídky platné “v tomto okamžiku” (u poptávky si to jakž takž představit umím).
Křivky se vůbec nemusí protnout. Kdy se neprotnou?
Křivka poptávky se může velmi rychle měnit v čase. Stačí pár zpráv o bakterii E-Coli a křivka poptávky po zelenině je na nějakou dobu úplně jinde, než byla.
Dejme tomu, že se křivky protínají a dokonce se ani nemění v čase. Rovnovážný bod existuje. Z průmyslovky si pamatuji, že regulovaná soustava nemusí vždy dokonvergovat k rovnovážné hodnotě. Také se může rozkmitat.
Samostatnou kapitolkou jsou státní zásahy do ekonomiky. Určitě znáte známé nařízení krále Já Prvního o tom, že se má veškerá sůl naházet to řeky. Bohužel o cenách soli na černém trhu po tomto zásahu pohádka nic nepraví. Zmiňuje se pouze o pokusu substituovat sůl smaragdem u ovcí.
A takhle se mi to v hlavě mele pořád … Přes to všechno věřím na protínání křivek nabídky a poptávky.
16/08/2011 v 11:19 pm
Tomášovi:
Kdyby tak lidé, kteří Vás potkávají, jak jdete po chodníku, věděli, co se Vám všechno honí hlavou!
Dovolil bych si z toho pro začátek vypíchnout dvě věci:
- místo uvažování o “kvantech” množství a ceny může být užitečné přemýšlet o poptávkové křivce pro jednotlivce (a třeba pro čepovatelnou komoditu, aby nás nerušila nespojitost) a potom se zamyslet, jaká by mohla vést cesta od poptávkových křivek jednotlivců k jakési agregované;
- ekonomika je opravdu složitý systém, takže není divu, že se z toho může točit hlava; půjde nám o to, jak ji vystihuje nebo nevystihuje ekonomie - budeme se držet při zemi, jen u úplných základů.
17/08/2011 v 1:59 pm
Mám v tom opravdu zmatek. Poptávka vyjadřuje objem zboží, které si chce kupující pořídit za danou cenu? Q je funkce P a osy by měli být obráceně. Nevidím, kde dělám chybu.
Ale nemyslím si, že křivka půjde asymptoticky k osám. Majetek na Zemi je omezen a nikdo nemůže zaplatit vyšší cenu. Od jisté ceny to bude nula. Co se týká osy Q, tak se křivka zlomí do záporných hodnot. Vždy bude existovat počet párků (zboží), při kterém už Vám další nepřinese žádný kladný užitek a naopak Vás začně obtěžovat (záporný užitek - záporná cena).
17/08/2011 v 2:33 pm
osy by měly
19/08/2011 v 9:42 am
Petrovi:
Zmatek v tom má kdekdo, proto se tomu také chceme věnovat.
V učebnicích ekonomie jsem většinou viděl “zákon klesající poptávky”, resp. poptávkovou křivku vysvětlovat tak, jak to říkáte - kolik zboží je kupující ochoten si pořídit za určitou cenu. Takže se to skutečně tváří, že poptávané množství je funkcí ceny. Pak by se ovšem dalo očekávat, že cena se bude vynášet cenu na vodorovnou osu.
V následujících článcích se toho dotknu, na říjnové instruktáži se tomu budu věnovat podrobněji.
Cesta k tomu vede ve směru, který jste se začal ubírat: přemýšlet o tom, jak by vypadala moje poptávková křivka po určitém produktu. Člověk si může zkusit vynášet relaci (proč by to hned měla být křivka?) znázorňující: za tuto cenu jsem ochoten koupit takovéto množství. V tu chvíli se začnou rojit problémy: včera, když bylo horko, by to bylo jinak než dnes, když je zima; mám hranici, nad kterou rozhodně nepůjdu, atd.
Celé to je hodně rozmazané. I ve fyzice se při výpočtech něco zanedbává, ale jistý druh zanedbávání vede k nesmyslům. Co se zanedbává zde a je to smysluplné?
A pak je třeba přemýšlet o “tržní poptávkové” křivce, o níž se v učebnicích říká, že vznikne součtem poptávkových křivek jednotlivců. Součtem malých rozmazaných fleků vznikne cosi jako křivka? Proč?
Snad je vidět, že stojí za to pátrat, zda se za tím skrývá nějaké rozumné vysvětlení. Přitom se také ukáže, proč se na obrázcích vynáší na vodorovné ose množství, ne cena.
20/08/2011 v 12:26 am
Pokud je to rozmazané, lze to interpretovat jako pravděpodobnost, že si zboží koupím za určitou cenu. Součet pro mnoho lidí bude opět distribuční funkce množství zboží při určité cene. Pokud budeme uvažovat dlouhý časový interval, tak bude důležitá střední hodnota, což vyjadřuje ta křivka.
20/08/2011 v 4:39 pm
Právě proto, že dnes mohou být jiné podmínky než včera, jsem mluvil o křivce nákladů v daném čase. Ale ani pro jednotlivce v jednom konkrétním okamžiku nemůžu vytvořit (najít?) poptávkovou křivku bez toho, že bych znal ceny ostatních produktů, které se mohou s daným produktem vzájemně zastupovat.
Příklad s párkem v rohlíku je tak sugestivní, že by člověk málem uvěřil, že s párkem v rohlíku se nedá dělat nic jiného, než ho sníst. Při vhodné konstelaci cen a podminek může mít párek v rohlíku mnoho dalších použití: mohu ho zmrazit a sníst později, může sloužit jako krmivo pro prasata, jako těžítko, jako dekorační předmět, jako hnojivo, jako pomůcka pro sportovní disciplínu “hod párkem v rohlíku”, v dostatečném množství by mohl posloužit k zablokování vchodu do úřadu vlády, po vysušení by se dal použít jako palivo, možná by se dal přidávat do benzínu (to nevím), propíchne-li se párek v rohlíku dvěma hřebíky ve vhodné vzdálenosti a zasune se do zásuvky 230V, pak v šeru svítí (tohle, prosím, nezkoušejte). A samozřejmě se dá prodat všem lidem, kteří chtějí jíst, krmit prasata, topit, trénovat disciplínu “hod párkem v rohlíku”, atd.
To pitná voda z vodovodu není tak sugestivní, tam bychom asi rychle odhalili, že se dá použít mnoha dalšími způsoby, než jen na uhašení žízně (viz spotřeba vody na hlavu).
Kdyby knihy byly zadarmo (vzdělání národa je třeba podporovat), asi by se v kamnech na tuhá paliva netopilo ničím jiným.
20/08/2011 v 4:56 pm
Tak myslím, že se mi předchozím příspěvkem podařilo ilustrovat pnu alternativu k výrazu “a tak dále” ve zmiňovaném textu:
>>Je to jako u křivky “mezního užitku”, která číhá v pozadí. Mám-li hlad, má pro mě párek v rohlíku velký užitek. Druhý párek už má menší užitek. Třetí párek má opět o něco menší (ale stále kladný) užitek. A tady se řekne “a tak dále”, jinak by se musely začít “kecat hlouposti”.
21/08/2011 v 8:42 pm
Petrovi:
není problém zkonstruovat jakýsi matematický model. Obtížné to začíná být v okamžiku, kdy se starám, zda to odpovídá něčemu reálnému. A tady mám s tím, co navrhujete, velké problémy. Uvedu to jenom telegraficky. Jako konkrétní případ budu brát koupi zmrzliny v horkém počasí. Koupím si 1, 2 nebo 3 kopečky (víc si rozhodně kupovat nebudu). Měl bych tedy u každé dvojice (c,k), kde c je cena a k počet kopečků uvést pravděpodobnost, a to tak, že součet všeho, co napíšu, dá součet 1. Něco musím uvést i u dvojice (0,0). To je jasně vidět u “poptávkové křivky” pro mrazivé počasí - tam si rozhodně žádnou zmrzlinu nekoupím, takže pravděpodobnost (0,0) bude 1 a všeho ostatního nula.
Zpět ke křivce z horkého dne. Opravdu nevidím, jaké hodnoty bych jednotlivým bodům měl přiřazovat. Například vezmu-li situaci, která není “rozmazaná” a já mám z jakéhosi neznámého důvodu naprosto jasno, za jakou cenu si tři možná množství zmrzliny koupím - budou tři nenulové body: (x,1), (y,2), (z,3). Mají mít všechny pravděpodobnost rovnu 1/3? Nebo pořadě například 0,2; 0,3; 0,5? Nebo ještě něco jiného? A opravdu musí pravděpodobnost (0,0) být nulová? Co to znamená? V tuto chvíli bych opravdu potřeboval pořádně definovat, co se myslí náhodným jevem, pro který se stanovuje pravděpodobnost. Já to nevidím.
Samozřejmě dovedu spočítat střední hodnotu (aritmetický průměr) údajů u jednotlivých dvojic z vedřinové a mrazové křivky. Jakou interpretaci mají? Dá se to rozumně napsat? A když to posčítám pro velké množství lidí …
Tomášovi:
1) Je pravda, že klesne-li cena šampaňského pod úroveň ceny vody, vzroste spotřeba šampaňského a klesne spotřeba vody, protože lidé se začnou v šampaňském koupat, mít nádobí, atd. S tím pracuje standardní způsob, jak se dochází k poptávkovým křivkám (například přes tečny k indiferenčním křivkám) a my to samozřejmě na instruktážích připomeneme.
Ale i zde se v okamžiku, kdy se řekne “a tak dále” musí začít “kecat hlouposti”. Jenom se to posune (třeba o pořádný) kus dál. (Třeba, až někdo začne vysvětlovat, že teď, když tak zlevnili párky, vyhodí své dosavadní těžítko a nahradí je párkem, nebo že ačkoli se bez těžítka dosud obešel, teď využije příznivé situace, aby si nějaké pořídil).
2) Mám pokušení začít logicky pitvat první z Vašich textů, ale připadá mi to jako hřích - tak krásné ty příklady jsou.
21/08/2011 v 10:26 pm
Přístup matematika.
Já bych se pokusil tu střední hodnotu změřit a pak bych zpětně hledal závislost na okolních jevech. Takže výsledek by byl. Při 30°C stupních si dám 0, 1 nebo 2 s pravděpodobnost 1/3. Při 25°C 0 - 2/3 1 - 1/3, 2-0. Atd.
22/08/2011 v 10:00 am
Fantastická diskuse.
Dovolím si trochu té letní diverze do Vašeho intelektuálního jiskření. Jedna z “murphologických pouček” - Ekonomové jsou lidé, kteří reálný svět vysvětlují pomocí modelů, v nichž je realita cosi jako mimořádná událost.